ABSTRACT
Automated Essay Scoring (AES) systems address the limitations of manual grading, such as inefficiency, subjectivity, and scalability issues in educational assessments, and this study evaluates the performance of lightweight BERT-based models for AES tasks, aiming to identify the most effective and computationally efficient variant for integration into a proposed AI Essay Score Bot by focusing on smaller, distilled transformer models to balance high accuracy with reduced resource demands, building on advancements in Natural Language Processing (NLP) from models like BERT, RoBERTa, and their variants. The publicly available ASAP-AES dataset was used, encompassing essays from prompts 1 to 8, with eleven small-scale BERT-based models tested: DistilBERT-base-uncased, DistilBERT-base-uncased-distilled-SQuAD, ALBERT-base-v1, ALBERT-base-v2, DistilRoBERTa-base, SqueezeBERT-uncased, SqueezeBERT-MNLI, SqueezeBERT-MNLI-headless, BERT-base-uncased, RoBERTa-base, and BORT; training involved a 5-fold cross-validation with 80% training and 20% validation splits, hyperparameter tuning across batch sizes (8, 16, 20), learning rates (1e-4, 3e-4, 3e-5, 4e-5, 5e-5), and epochs (5, 10, 15, 20), while the EXPATS toolkit facilitated model implementation, training, and evaluation under an in-domain schema, with performance measured using the Quadratic Weighted Kappa (QWK) metric. DistilBERT-base-uncased achieved the highest average QWK of 0.926 (batch size 16, 10 epochs), outperforming others across most prompts, with improvements noted in hyperparameter configurations (e.g., learning rate 3e-5), while ALBERT-base-v1 followed closely with a maximum QWK of 0.920 (batch size 8, 20 epochs), despite GPU memory constraints limiting batch sizes; smaller models like DistilRoBERTa-base (average QWK 0.907) and SqueezeBERT-uncased (0.910) surpassed larger counterparts such as BERT-base-uncased (0.903) and RoBERTa-base (0.860), with prompts 1 and 7 consistently challenging, where SqueezeBERT-uncased scored highest on Prompt 1 (QWK 0.880) and SqueezeBERT-MNLI on Prompt 7 (0.780), and underperforming models included BORT (average 0.770) and ALBERT-base-v2 (0.830), affected by architectural simplifications. The superior performance of distilled models like DistilBERT and ALBERT underscores the benefits of knowledge distillation and parameter optimization techniques, enabling better QWK scores with lower computational overhead compared to full-sized BERT and RoBERTa, with batch size increases (up to 20) enhancing DistilBERT variants, particularly on difficult prompts, while ALBERT’s efficiency stemmed from factorized embeddings and cross-layer sharing; challenges on Prompts 1 and 7 suggest dataset-specific complexities, such as varied essay structures, indicating that lightweight models are ideal for resource-limited applications, though further distillation of ALBERT could yield even more compact variants without sacrificing precision. Distilled transformer models, especially DistilBERT-base-uncased and ALBERT-base-v1, offer an optimal trade-off between accuracy and efficiency for AES tasks, making them suitable for real-world deployment in web-based AI tools, and future research should investigate distilling ALBERT to enhance compactness and explore transfer learning for cross-domain AES improvements.
INTRODUCTION
Automated Essay Scoring (AES) has emerged as a critical area of study within educational assessment, addressing the limitations of manual grading processes, which are time-consuming and prone to subjectivity (Page, 1966). Early AES systems relied on rule-based approaches, such as Project Essay Grade (PEG) developed by Ellis Batten Page in the 1960s (Page, 1967). These systems, while pioneering, lacked the ability to capture the complexities of language and context effectively. The advent of Natural Language Processing (NLP) and machine learning techniques has led to significant advancements in AES. Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks have been instrumental in capturing sequential dependencies in text data (Hochreiter and Schmidhuber, 1997). Furthermore, transformer-based architectures, such as Bidirectional Encoder Representations from Transformers (BERT), introduced by Devlin et al., (2018), have revolutionized AES research by enabling models to capture contextual information bidirectionally.
Studies have demonstrated the effectiveness of BERT in various NLP tasks (Devlin et al., 2018), including sentiment analysis (Sun et al., 2019), named entity recognition (Jin et al., 2019), and document classification (Lee et al., 2019). BERT’s ability to pre-train on large corpora of text data and fine-tune on task-specific datasets has contributed to its success in AES tasks (Devlin et al., 2018). In addition to BERT, other transformer-based architectures, such as Generative Pre-trained Transformer (GPT) developed by OpenAI, have shown promise in AES research (Radford et al., 2018). GPT’s ability to generate coherent text and make contextually relevant predictions can be leveraged for scoring essays (Radford et al., 2018).
Overall, the integration of deep learning techniques, particularly transformer-based models like BERT and GPT, represents a significant advancement in AES research, offering improved accuracy and scalability compared to traditional approaches.
METHODOLOGY
Evaluation Metrics
The primary evaluation metric for our AES models is the Quadratic Weighted Kappa (QWK), which serves as an agreement metric, ranging from 0 to 1. Negative values indicate less agreement than expected by chance. QWK is utilized to report the performance of our models on each prompt, the official metric for the ASAP-SAS competition, to provide a concise summary of performance across prompts.
Evaluation Schemas
We employ in-domain evaluation scheme. In an in-domain evaluation, the system is trained and evaluated on the same prompt, while a cross-domain evaluation involves training and evaluating the system on different prompts. This approach assesses AES systems employing transfer learning techniques.
Data Preparation and Model Training
Model training employs a 5-fold cross-validation approach with separate train/validation/test splits. The official ASAP-SAS training data are divided into 5 folds, with 80% allocated for training and 20% for validation. A batch size of {8, 16, 20} and the learning rate is tuned within the range of {1e-4, 3e-4, 3e-5, 4e-5, 5e-5}. During hyperparameter tuning, the model’s performance is evaluated solely on the validation sets, recording the best performance achieved across epochs range of {5, 10, 15, 20}. The training process stops at the specified ranges of epoch across the validation folds. After hyperparameter tuning, the final models are trained by combining the training and validation sets.
Automated Text Scoring Toolkit
For this study, we employed EXPATS (Manabe and Hagiwara 2021), an automated text scoring toolkit designed for a variety of Automated Text Scoring (ATS) tasks, including automated essay scoring and readability assessment. EXPATS is an open-source framework that facilitates the rapid development and experimentation of diverse ATS models through its user-friendly components, configuration system, and command-line interface. Moreover, the toolkit seamlessly integrates with the Language Interpretability Tool (LIT), enabling users to interpret and visualize models along with their predictions.
EXPERIMENTATION
BERT-based models
Our initial experiment aimed to assess the performance of various small BERT-based models, including distilbert-base-uncased, distilbert-base-uncased-distilled-squad, albert-base- v1, albert-base-v2, distilroberta-base, squeezebert-uncased, squeezebert-mnli, squeezebert-mnli-headless, bert-base- uncased, roberta-base, and BORT. DistilBERT-base-uncased is a distilled version of BERT designed to be smaller and faster while retaining much of BERT’s performance across NLP tasks, using a transformer-based architecture for pre-training on large text corpora. DistilBERT-base-uncased-distilled-SQuAD builds on this by being specifically optimized for question-answering through additional distillation on the SQuAD dataset. ALBERT-base-v1 introduces parameter reduction techniques for efficiency without compromising performance, while ALBERT-base-v2 further enhances this with improved dropout and broader training data. DistilRoBERTa-base is a compact version of RoBERTa that maintains effectiveness with a smaller model size. SqueezeBERT-uncased offers a compressed BERT model for resource-constrained settings via pruning and quantization, and its variant, SqueezeBERT-MNLI, is tailored for natural language inference tasks. SqueezeBERT-MNLI-headless removes the task-specific classification layer for flexible downstream use. BERT-base-uncased is the original benchmark transformer model for bidirectional text representations. RoBERTa-base extends BERT with enhanced training strategies and data processing for improved task performance. Finally, BORT is designed for efficient inference, leveraging quantization, pruning, and sparse attention to minimize computational load, albeit with some trade-offs in accuracy. Our objective is to identify the smallest model capable of achieving optimal performance in our future AES application, as determined by the highest average Quadratic Weighted Kappa (QWK) score.
Models Evaluation
All models were trained for 10 epochs with a learning rate of 4e-5 and a validation ratio of 0.2. The DistilBERT-base-uncased and DistilBERT-base-uncased-distilled-SQuAD models were evaluated using batch sizes of 8, 16, and 20. DistilRoBERTa-base was trained using batch sizes of 8 and 16.
The remaining models-ALBERT-base-v1, ALBERT-base-v2, SqueezeBERT-uncased, SqueezeBERT-MNLI, SqueezeBERT-MNLI-headless, BERT-base-uncased, RoBERTa-base, and BORT-were all trained with a batch size of 8. Initially, the learning rate was set to 4e-5, with 10 epochs and a validation ratio of 0.2. Due to the limited GPU memory size of our 3080TI 12GB GPU, batch sizes varied among models. Specifically, models such as albert-base-v1, albert-base-v2, squeezebert-uncased, squeezebert-mnli, squeezebert-mnli-headless, bert-base- uncased, roberta-base, and bort encountered “GPU memory full” errors when batch sizes exceeded 8. In contrast, distilbert-based models could handle batch sizes up to 20, while distilroberta could manage up to a batch size of 16 without errors. These findings indicate that distilled-based techniques produce smaller models compared to the original BERT model and others Lite BERT Model, allowing for larger batch sizes and more efficient GPU memory usage.
Table 1 reveals that the distilbert-base-uncased model exhibited superior performance across prompts 2, 3, 4, 5, 6, and 8, with an average Quadratic Weighted Kappa (QWK) score of 0.918. The Albert-base-v1 model, which ranked second, achieved an average QWK score of 0.914. These results surpass those of the original Bert-base-uncased model, which recorded a QWK of 0.903. Even smaller models, such as distilroberta-base and squeezebert-uncased, outperformed the original BERT-based model. However, prompts 1 and 7 posed significant challenges for most models. The squeezebert-uncased model achieved the highest QWK for Prompt 1 with a score of 0.880, while the squeezebert-mnli model scored 0.780 for Prompt 7. The bottom three performing models were bort (negatively impacted by prompts 5 and 7), albert-base-v2 (affected by prompts 1 and 7), and roberta-base (affected by prompt 7). Notably, the BORT model performed the worst, likely due to being overly simplified. Similarly, the performance of the latest version of albert-base-v2 deteriorated compared to its older v1 version likely due to changes on the dropout ratio and tuned to larger and more diverse data.
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | Avg | |
|---|---|---|---|---|---|---|---|---|---|
| Model | Bert Based Model with Batch Size=8 | ||||||||
| Distilbert-Base- Uncased | 0.88 | 0.94 | 0.94 | 0.97 | 0.961 | 0.97 | 0.75 | 0.95 | 0.92 |
| Distilbert-Base- Uncased-Distilled-Squad | 0.87 | 0.93 | 0.92 | 0.96 | 0.956 | 0.95 | 0.74 | 0.94 | 0.91 |
| Albert-base-v1 | 0.86 | 0.93 | 0.93 | 0.97 | 0.958 | 0.96 | 0.78 | 0.94 | 0.91 |
| Albert-base-v2 | 0.63 | 0.93 | 0.89 | 0.96 | 0.839 | 0.95 | 0.56 | 0.92 | 0.83 |
| Distilroberta-base | 0.85 | 0.94 | 0.93 | 0.96 | 0.96 | 0.96 | 0.72 | 0.94 | 0.91 |
| Squeezebert- uncased | 0.88 | 0.92 | 0.93 | 0.96 | 0.897 | 0.95 | 0.78 | 0.92 | 0.91 |
| Squeezebert-mnli | 0.84 | 0.85 | 0.9 | 0.94 | 0.951 | 0.95 | 0.78 | 0.9 | 0.89 |
| Squeezebert-mnli-headless | 0.85 | 0.92 | 0.92 | 0.95 | 0.946 | 0.96 | 0.74 | 0.92 | 0.9 |
| Bert-Base- uncased | 0.85 | 0.93 | 0.93 | 0.97 | 0.959 | 0.96 | 0.7 | 0.92 | 0.9 |
| Roberta-base | 0.84 | 0.93 | 0.82 | 0.96 | 0.952 | 0.91 | 0.57 | 0.93 | 0.86 |
| Bort | 0.85 | 0.93 | 0.94 | 0.96 | 0.009 | 0.96 | 0.64 | 0.91 | 0.77 |
| Model | Distilbert Based Model with Batch Size=16 and 20 | ||||||||
| Distilbert-base- uncased (16) | 0.89 | 0.94 | 0.94 | 0.97 | 0.958 | 0.96 | 0.82 | 0.93 | 0.93 |
| Distilbert-base- uncased-Distilled- squad (16) | 0.88 | 0.93 | 0.94 | 0.97 | 0.964 | 0.96 | 0.71 | 0.93 | 0.910 |
| Distilroberta-base (16) | 0.85 | 0.94 | 0.92 | 0.96 | 0.952 | 0.96 | 0.74 | 0.87 | 0.9 |
| Distilbert-base- uncased (20) | 0.83 | 0.93 | 0.94 | 0.97 | 0.96 | 0.96 | 0.83 | 0.9 | 0.92 |
| Distilbert-base- uncased-Distilled- squad (20) | 0.86 | 0.93 | 0.94 | 0.96 | 0.96 | 0.96 | 0.84 | 0.92 | 0.920 |
Table 1 also presents the evaluation results for distilbert-base-uncased, distilbert-base-uncased-distilled-squad, and distilroberta-base, which is the third best-performing model. We aimed to verify whether varying batch sizes could enhance their performance. The overall results indicate that distilbert-base-uncased achieves the highest average QWK of 0.926 with a batch size of 16, while distilbert-base-uncased- distilled-squad achieves an average QWK of 0.920 with a batch size of 20. These improvements in the distilbert models are primarily due to increased QWK scores on prompt 7, with slight effects on the QWK scores of other prompts. However, the performance of distilroberta-base decreases from a QWK of 0.907 to 0.898 when the batch size is increased from 8 to 16. Despite this, distilroberta-base still outperforms its original roberta-base counterpart. The improvements observed in the smaller distilbert and distilroberta models compared to their larger BERT and ROBERTA parent models suggest that the distillation method (Hinton et al., 2015) is a significant factor in achieving better QWK results. Additionally, as shown in Table 1, the Albert-base-v1 model produced commendable QWK results, even outperforming bert-base, roberta-base, and some other distilled models for prompts 1 and 7. Therefore, we presume that a distilled Albert-base-v1 model would be able to achieve better QWK scores than the distilbert and distilroberta models. Consequently, we decided to conduct further investigation into hyperparameter tuning for the distilbert and Albert v1- based models.
Distilbert and Albert Model Evaluations
The subsequent evaluation process for the distilbert and albert models was repeated across 5, 10, 15, and 20 epochs based on a hyperparameter configurations. The hyperparameter configurations consist of ten different combinations of learning rates and batch sizes. Configurations 1 through 5 use a batch size of 8, with learning rates of 4e-5, 3e-5, 5e-5, 3e-4, and 1e-4, respectively. Configurations 6 through 10 use the same learning rates in the same order but with a batch size of 16 instead. These combinations are designed to explore the effect of varying learning rates and batch sizes on model performance. However, for the albert model the batch size limitation is up to 8.
The results presented in Figures 1 and 2 indicate that achieving an epoch count of 10 or higher yields favourable QWK outcomes for both models. Conversely, configuration 4, which employs a Learning Rate (LR) of 3e-4 and a batch size of 8, consistently demonstrates poor performance across all epoch settings for both models. Similarly, configuration 9 (LR 3e-4, batch size 16) is suboptimal for the distilbert model; although higher epochs improve the QWK, the results remain significantly lower than other configurations.
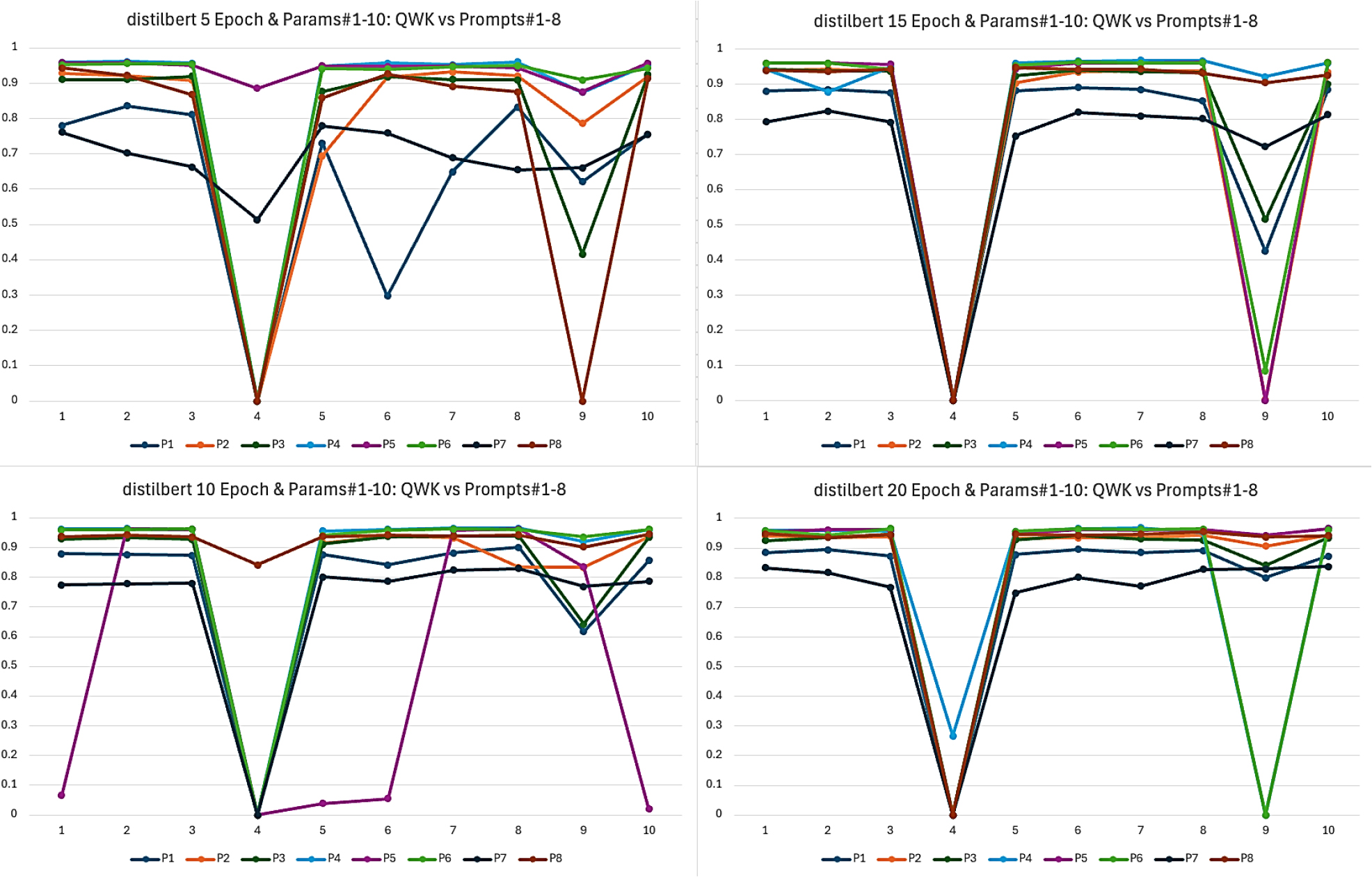
Figure 1:
Distilbert hyperparameter 1 to 10 results.
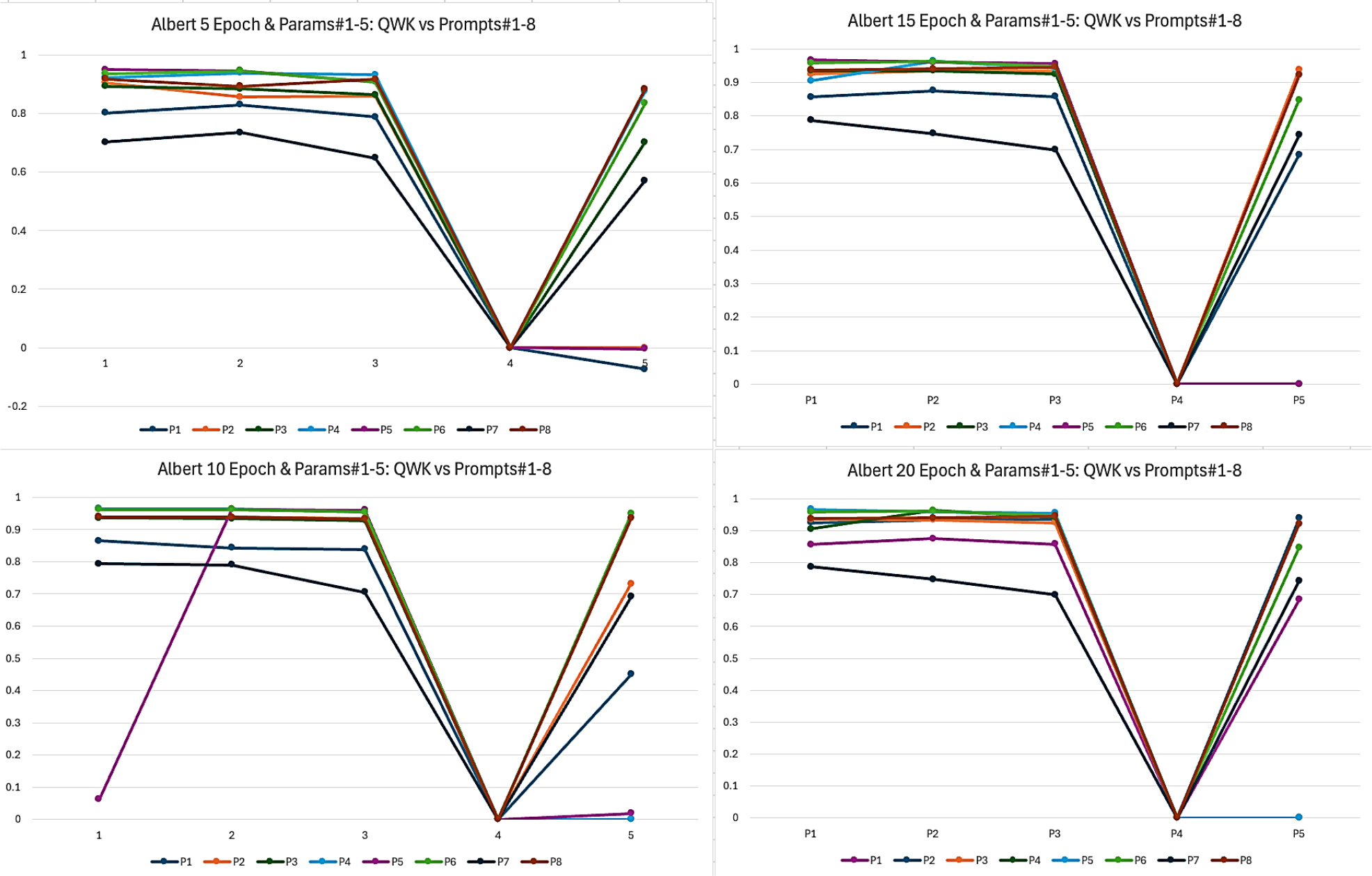
Figure 2:
Albert hyperparameter 1 to 5 results.
Configuration 5, with an LR of 1e-4 and a batch size of 8, also shows unsatisfactory QWK results for the Albert-base model, but increasing the epoch to 20 raises the QWK to 0.844. Table 2 indicates the QWK results at epoch 20 for the distilbert model exhibit stability, averaging 0.926 across most configurations, with the highest QWK of 0.928 occurring under configuration 6 (LR=3e-5, batch size=16). For the Albert model, QWK results are stable at an average of 0.915 at epoch 15, with the highest QWK of 0.92 achieved under configuration 3 (LR=5e- 5, batch size=8) at epoch 20. The results shows that even though without been distilled and batch size only max at 8, Albert performance is comparable with distilbert.
| Prompt | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | Avg |
|---|---|---|---|---|---|---|---|---|---|
| Setting | Distilled-base-uncased | Epoch 5 | |||||||
| 1 | 0.781 | 0.929 | 0.911 | 0.959 | 0.958 | 0.952 | 0.761 | 0.943 | 0.899 |
| Epoch 10 | |||||||||
| 7 | 0.882 | 0.933 | 0.94 | 0.965 | 0.958 | 0.963 | 0.824 | 0.939 | 0.926 |
| Epoch 15 | |||||||||
| 6 | 0.891 | 0.936 | 0.94 | 0.966 | 0.96 | 0.964 | 0.821 | 0.942 | 0.928 |
| 7 | 0.886 | 0.938 | 0.937 | 0.969 | 0.961 | 0.96 | 0.81 | 0.944 | 0.926 |
| Epoch 20 | |||||||||
| 6 | 0.896 | 0.935 | 0.944 | 0.966 | 0.962 | 0.964 | 0.801 | 0.942 | 0.926 |
| 8 | 0.891 | 0.942 | 0.926 | 0.952 | 0.961 | 0.964 | 0.828 | 0.954 | 0.927 |
| 8 | 0.891 | 0.942 | 0.926 | 0.952 | 0.961 | 0.964 | 0.828 | 0.954 | 0.927 |
| 10 | 0.872 | 0.942 | 0.935 | 0.965 | 0.965 | 0.961 | 0.838 | 0.941 | 0.927 |
| 1 | 0.884 | 0.941 | 0.925 | 0.959 | 0.955 | 0.959 | 0.833 | 0.948 | 0.926 |
| Setting | albert-base-v1 | Epoch 5 | |||||||
| 1 | 0.802 | 0.906 | 0.894 | 0.924 | 0.95 | 0.936 | 0.703 | 0.919 | 0.879 |
| 2 | 0.83 | 0.857 | 0.884 | 0.939 | 0.946 | 0.947 | 0.735 | 0.893 | 0.879 |
| Epoch 10 | |||||||||
| 2 | 0.843 | 0.938 | 0.934 | 0.964 | 0.963 | 0.963 | 0.79 | 0.938 | 0.917 |
| Epoch 15 | |||||||||
| 1 | 0.856 | 0.925 | 0.935 | 0.905 | 0.966 | 0.958 | 0.787 | 0.937 | 0.909 |
| 2 | 0.875 | 0.934 | 0.934 | 0.963 | 0.96 | 0.962 | 0.747 | 0.94 | 0.915 |
| Epoch 20 | |||||||||
| 1 | 0.856 | 0.925 | 0.935 | 0.905 | 0.966 | 0.958 | 0.787 | 0.937 | 0.909 |
| 2 | 0.875 | 0.934 | 0.934 | 0.963 | 0.96 | 0.962 | 0.747 | 0.94 | 0.915 |
CONCLUSION
RoBERTa (Liu et al., 2019) is a more complex model compared to the original BERT due to its increased number of parameters, which result from training on a larger dataset and possibly incorporating additional layers. As shown in Table 1, BERT (Devlin et al., 2019) outperforms RoBERTa, suggesting that the AES-ASAP dataset benefits from smaller models. However, the distilled version of RoBERTa (DistilRoBERTa) surpasses BERT in performance, indicating that a smaller model, further optimized through distillation, is even better suited for AES-ASAP data.
ALBERT, a lite variant derived from BERT, is designed to reduce model size and enhance efficiency while preserving performance. ALBERT achieves this by employing factorized embedding parameterization and cross-layer parameter sharing, which reduces the number of parameters and improves performance on AES-ASAP data, surpassing its predecessor, BERT, and DistilRoBERTa (Sanh et al., 2019).
DistilBERT (Sanh et al., 2019) is another variant that utilizes knowledge distillation, where a smaller model (the student) is trained to replicate the behavior of a larger model (the teacher). In this case, the teacher model is the original BERT. DistilBERT reduces the number of layers by approximately 50%, while retaining the same hidden size and other architectural parameters to maintain a significant portion of the original model’s performance.
Applying distillation to ALBERT (Lan et al., 2020), which already benefits from parameter sharing and factorized embedding parameterization, could potentially result in an even more compact model. This model would be faster and require less memory during inference for AES data, while still retaining a high level of performance. Distillation is thus an effective method to preserve performance in a smaller model, compared to merely reducing the number of layers or parameters without the guidance of a teacher model.
Cite this article:
Noor MNMM, Badauraudine MFM. Evaluating Small BERT Based Models on Automated Essay Scoring Task. Info Res Com. 2025;2(2):175-81.
ACKNOWLEDGEMENT
This research is supported by Universiti Kuala Lumpur MIIT Research and Innovation Section.
References
- A lite BERT for self-supervised learning of language representations.. Google Scholar
- Pre-training of deep bidirectional transformers for language understanding.. : 4171-4186 Google Scholar
- Devlin J., Chang M. W., Lee K., Toutanova K.. (2018) BERT: Pre-training of deep bidirectional transformers for language understanding. Google Scholar
- Hochreiter S., Schmidhuber J.. (1997) Long Short-Term Memory. Neural Computation 9: 1735-1780 Google Scholar
- DistilBERT, a distilled version of BERT: Smaller, faster, cheaper, and lighter Google Scholar
- Hinton G., Vinyals O., Dean J.. (2015) Distilling the knowledge in a neural network. Google Scholar
- Jin D., Jin Z., Zhou J., Szolovits P.. (2019) Multi-channel BERT for named entity recognition. Google Scholar
- Lee J., Yoon W., Kim S., Kim D., Kim S., So C. H., Kang J., et al. (2020) BioBERT: A pre-trained biomedical language representation model for biomedical text mining. Bioinformatics 36: 1234-1240 https://doi.org/10.1093/bioinformatics/btz682 | Google Scholar
- Manabe H., Hagiwara M.. (2021) EXPATS: A toolkit for explainable automated text scoring. https://doi.org/10.1093/bioinformatics/btz682 | Google Scholar
- Open A. I.. 2024 ChatGPT [Large language model].
- Page E. B.. (1966) The project essay grade (PEG) system: Automation of essay scoring. Educational Technology 6: 20-24 https://doi.org/10.1093/bioinformatics/btz682 | Google Scholar
- Radford A., Narasimhan K., Salimans T., Sutskever I.. 2018 Improving language understanding by generative pre-training.
- RoBERTa: A robustly optimized BERT pretraining approach. https://doi.org/10.1093/bioinformatics/btz682 | Google Scholar
- Sun C., Qiu X., Xu Y., Huang X., Zhang Y., Wei F., et al. (2019) How to fine-tune BERT for text classification?. https://doi.org/10.1093/bioinformatics/btz682 | Google Scholar

